版权声明：文章观点仅代表作者观点，作为参考，不代表本站观点。部分文章来源于网络，如果网站中图片和文字侵犯了您的版权，请联系我们及时删除处理！转载本站内容，请注明转载网址、作者和出处，避免无谓的侵权纠纷。
其他百科
当前位置：首页 > 百科知识 > 其他百科
韦布尔方程
作者：佚名 来源于：学习力教育中心
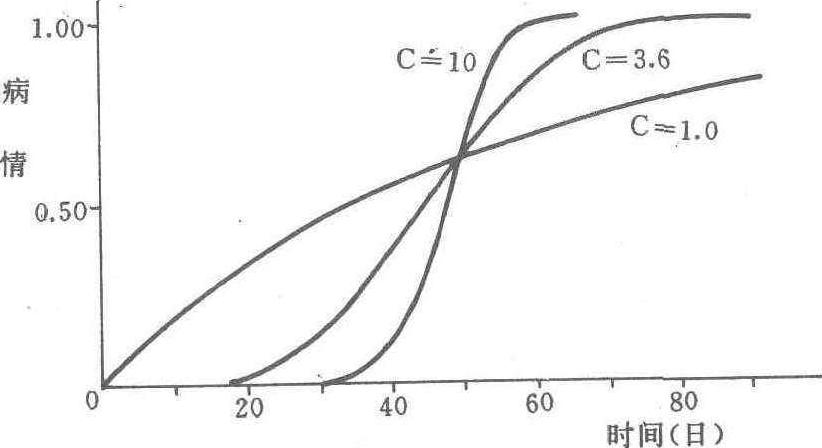
概率密度函数之一。彭尼帕克(Pennypacker，1980)将其引入植病流行学中病害季节性流行动态的研究，其微分形式为：
dX/dt=c/b(t-a/b)(c-1)exp[-(t-a)/b]c
积分形式可写成：Xt＝1-exp{-(t-a)/b〕c}
(b>0，c>0，t>a)
式中 Xt为时间t时的病情百分率;a为位置参数，决定病害始发期;b为比率参数，决定流行速度;c为流行曲线的形状参数，决定流行的先后速度的相对快慢。由于方程有三个参数，其种种组合可描述多种形式的流行曲线，因此也称弹性模型(flexible model)。当c=1时，韦布尔方程可代替指数模型用来描述单年病害流行。当c=3.6时可代替逻辑斯蒂模型用于描述单年流行病害的流行。式中的a为病害数量开始增长的日期。因 ......
上一篇： 微梯弗利亚效应
下一篇： 魏景超
韦布尔方程 农业百科 百科知识
百科知识
农业百科
民间故事
中国儿童文学网
中国童话故事
传说
故事
教育发展史
格林童话
格林童话故事全集
格林童话故事
格林
孩子
中国
安徒生
安徒生童话
家庭教育
美国
彝族
(一)发展历程
【相关文章】
